Blog
Bayesian Data Analysis: A brave “new” world of statistics
May 14, 2021 | Chris Kervinen

There has been a lot of discussion around the Bayesian approach in Marketing Mix Modeling, with some of the most data-savvy companies and agencies doubling up their investments in this methodology. Today we'll break down what it is, where it came from and what is the benefit of it.
We’ve previously talked about Marketing Mix Modeling and cars , and how different alternatives have their counterparts in both worlds. And believe it or not, similarities of this odd couple don’t end up just there. But instead of comparing what kind of cars there are, today we’re taking a look under the hood and reviewing what principles make the machine move so fast.
Today, we’re breaking down the pros and cons of the Tesla of MMM.
Like electric cars, Bayesian statistics isn’t a new phenomenon per se. Named after the father of the theorem Thomas Bayes, the approach was first published in 18th century. Likewise, first electric cars were produced at the late 19thcentury. Unfortunately, similar fate met both of these visionary concepts, as the technological development did not support larger-scale implementation of either electric cars or Bayesian methods at time.
What made statisticians dislike the Bayesian methods was the amount of computation they required to complete, which made the frequentist interpretations a much more practical choice at that time.
Fastforward to today, computers’ computational power combined with powerful algorithms, such as Markov chain Monte Carlo, has enabled Thomas’ idea to reach its full potential.
Thomas’ idea
Thomas Bayes was a statistician as well as a philosopher from 1700s England. He has only two works published during his lifetime, of which neither relate to his far more known, posthumous legacy.
During his later years, however, Thomas immersed himself into world of probability. Although at time Thomas was very ill, he managed to gather his thoughts in a manuscript that would later on get finalized and published in 1763 with help of his friend Richard Price.
The theory has been developed further by various authors, such as Pierre-Simon Laplace, Sir Harold Jeffreys & Stephen Stigler. In its simplest from, Bayes’ theorem itself can be stated as follows:
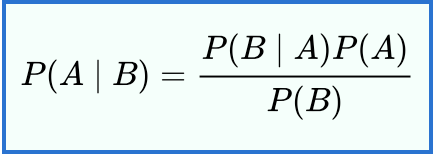
In which:
· P(AI B) is the probability if A occurring given that B is true
· P(BI A) is the same but vice versa
· P(A)& P(B) are probabilities for events A and B happening
In other words, Bayes’ theorem allows us to systematically draw conclusions based on gathered data and prior experience or expectations.
In Thomas’ mindset probabilities could and would be estimated more realistically by looking at the bigger picture. This makes the model far more capable compared to traditional modeling techniques, but only in the right hands.
Risks and rewards of Bayesian modeling
Compared to previous generations, there are three major differences in Bayesian modeling that need to be considered to avoid jumping into a world of trouble: Priors, Hierarchical modeling & probabilistic programming tools. The two first enable Bayesian approach to deliver superior accuracy and reliability in terms of the results, whereas the third describes how extremely complex calculations can be run in practice.
1. Priors
Being able to set priors is one of the most powerful, yet dangerous feature in the Bayesian modeling. When done correctly, priors have two distinctive advantages:
1. They provide intervals for expected results to help in fitting the data, and
2. They enable modeling with fewer datapoints
Providing guidelines for the modeling outcomes helps the model to “look for the results” from the right places, instead of assuming anything’s possible. This can obviously be a double-edged sword, as miscalculations in the priors can and will ruin the whole modeling in the first place.
Roughly speaking, it’s like refueling your Tesla with gasoline.
So what it takes to set up the priors accordingly, then?
In addition to technical know-how, business intelligence is also required. These insights can come from the modeler, but it can also be integrated into the model by an internal or external expert.
The outcome should look something like this:
As can be seen, the priors help the model to avoid results that are inconsistent or in conflict with previous learnings and knowledge. This introduces continuity to analytics as a process and becomes especially handy when dealing with smaller datasets (which are an inevitable side effect of doing the modeling on more granular level).
Usually, when the number of data points increases, so does the accuracy and reliability of the modeling results. But when the number of variables increases (let’s say you want to know the ROMI for all channels within TV media group instead of average TV ROMI, include weather as a factor and isolate promotions’ effect on sales), traditional models start to experience difficulties in providing reliable results and neglecting noise.
Similar issues arise when there’s new variables, for example new media channels at play. The newness of variables results data scarcity, which in turn can generate huge variation in the results.
The solutions:
Business priors that narrow down possible outcomes, so that the model can manage with less data. A relevant example of this are the Covid-19 infection trajectories , where there’s relatively little data, but by leveraging previous records from epidemics and pandemics as priors, the model can provide stronger insights than traditional models.
2. Hierarchical modeling
Hierarchical modeling is, as the name suggests, writing the model on multiple levels in which the sub-models can be gathered under higher-level models, eventually forming one hierarchical model. It’s somewhat like a Ponzi scheme, except everyone wins (equally) in hierarchical modeling.
By building one comprehensive model instead of multiple separate models the results will be more consistent with each other. Moreover, as Bayes’ theorem is applied in the hierarchical modeling, the results will be consistent with prior learnings as well.
Hierarchical models’ consistency provides a crucial solution for situations when there’s multiple media dimensions at play.
Let’s say you’ve been assigned to model previous campaign’s commercial performance. Both the marketing and sales data is in prime form, and you’ve been lucky enough to get it all for the modeling project. The problem is, however, that in addition to the usual media mix, the campaign manager has decided to throw a new TV channel to the mix.
With data from only a few weeks, it is practically impossible to get reliable results by modeling this new channel separately. But by applying hierarchical modeling, the “TV parent prior” tells the model how TV as a media channel usually behaves, and what kind of variation there are in the sub-models.
This might sound like the model is “forced” to generate desired outcomes, but we assure no model was harmed upon writing this article (or any of Sellforte’s models). Moreover, the model has been proven to be robust in empirical tests.
Another unparalleled benefit of the hierarchical models is their ability to manage multiple sales dimensions as well.
Example time!
You’re modeling TV’s effectiveness in the last campaign. You could run the model for fish and fruit products separately, but you decide not to do so as this approach has a possibility to end up with very different ROMI metrics for TV. Instead, as both fish and fruit products belong to grocery-group, you “tell” the model that because of this, TV should behave similarly for both subgroups.
After learning the power of hierarchical models, you don’t stop at the media and sales dimensions – you expand the dimensionality to campaigns as well! You tell the model that specific media channel should have similar behavior across different campaigns, given some variation.
“But this feels a bit forced…”
It is true that priors can steer badly written models or too scarce datasets to predefined direction. But so does every other model. Because whether you like it or not, every model includes assumptions, and the priors in Bayesian modeling just make these assumptions more visible. And like mentioned in the beginning, it is highly advised to have either own business intuition, or acquire via colleague.
Unfortunately, including priors and writing the model in hierarchical form makes the calculations far more complex than usual. So much more complex, that the normal analytical approaches won’t cut it anymore.
As the calculations grow massive, it’s no longer applicable to utilize analytical approach. Photo by ThisIsEngineering
Just like it’s no longer applicable to install Model 3’s engine to the Cybertruck, you need something far more powerful to run these new generation models.
Something more powerful like Probabilistic Programming Tools.
3. Probabilistic Programming Tools
Markov chain Monte Carlo (MCMC), Automatic Differentiation Variational Inference (ADVI), Maximum a Posteriori Probability (MAP). Here’s some of the most known methods for pulling numbers out of the extremely complicated calculations Bayesian modeling requires.
You know when teenagers describe their relationship drama, it’s usually “extremely complicated”.
When we say the calculations required in the Bayesian modeling are extremely complicated, it’s a bit beyond that.
In fact, they’re so complicated that there isn’t any analytical solution that would be able to manage all that complexity that the hierarchical models produce.
How the above-mentioned methods bypass this dilemma is they draw samples from the distribution of a continuous random variable. These sets of samples are generated by chains of points moving around the desired distributions according to [random / stochastic], but carefully engineered algorithmic steps.
From outside-in, it’s a like blockchain. In a way that sounds simple, but in practice it’s probably something different than what most of us assume it to be.
Another good characterization of the probabilistic programming methods is the software their utilized in, Stan , which was named by the great Stanislav Ulam – who collaborated in the Manhattan Project and innovated fusion bomb. Talk about making an impact.

One of the most common probabilistic programming language Stan was named after Stanislaw Ulam, who also pioneered e.g. the Monte Carlo method and fusion bomb. Image by WikiImages
All in all, the setup that enables calculations on this scale is massive. Which is one of the first problems people encounter when striving towards Bayesian modeling.
To overcome this obstacle, the modeler can either shorten the amount of moves the chain makes or avoid random walk behavior altogether. Since these compromises can hinder the convergence to the desired distribution, they tend to set high requirements for both the modeler and his/her understanding of the MCMC methods as well as the computational tools and platforms.
And just like with the business priors, great power comes with great responsibility in probabilistic programming as well. The process requires substantial computational power, something only the latest technological advancements have made possible. Most modelers resort to cloud-based platforms such as Amazon Web Services or Microsoft Azure, as they provide means to do the modeling without investing in supercomputers and data centers.
Great Leap Forward
There are fascinating historical examples of how progress is inevitable, yet extremely elusive. Around 1960, China and South Korea were both on a brink of change. As globalization was catching up, both governments knew they had to either evolve or fall behind in the international economical development.
They also knew that to accelerate the change, private sector had to aligned with the state objectives. Based on the two approaches each country chose, very different outcomes unfolded in terms of economy, growth, and happiness.
China decided to fit the economy into a mold without including prior learnings, privatizing majority of the physical capital in the country. South Korea on the other hand chose to modify the mold based on prior knowledge and build hierarchies around export and innovation.
As a result, South Korea’s economy leapt to the top of global charts, whereas China’s government was completely lost due to wildly inaccurate and unrealistic statistics.
Today, companies are facing similar leap of progress.
As technology enables new powerful methods like Bayesian modeling, companies must make sure they have both physical and human capital to enable the leap.
Continuing with the traditional methods when you’re doing fine business-wise might seem like a risk-free option. But in our intensively competed world it’s not how fast you’re running per se, it’s how fast you’re running compared to your competitors.
Change isn’t, however, easy. Change requires uncertainty, perseverance, and letting go of the old.
Change is also inevitable. Those that tap into the change evolve and leap forward, whereas others will be left behind. This can be already seen with 99% of Fortune 1000 companies reporting investment in data and AI.
Electric cars and Bayesian modeling are both finally here to stay. The question is, will you be on the driver’s seat?
Curious to learn more? Book a demo.
Related articles
Read more postsNo items found!