Blog
Automatic differentiation, differentiable programming, and Bayes
December 14, 2021 | Dr. Juha Kreula, Senior Data Scientist
Automatic differentiation (AD, also called algorithmic differentiation) is an algorithmic approach to automatically evaluate the gradient of functions that are implemented as computer programs.
It is one of the major reasons behind the success of training deep neural networks with multiple hidden layers. It also plays an important role in modern Bayesian statistical methods that use gradient information for learning. Differentiable programming is a recent umbrella term for the various AD techniques and use cases.
Despite its impact in training machine learning models, automatic differentiation is not often covered in machine learning courses and textbooks beyond a mention. The aim of this post is to shed some light on this topic.
Automatic differentiation in a nutshell
What is it (not)?
Automatic differentiation is one of the key tools behind the wide adoption of numerous machine learning methods where gradient information is used for training the model. Notably, AD is used for instance in the Tensorflow and PyTorch libraries for training deep neural networks via the backpropagation algorithm.
Automatic differentiation also plays an important role in modern probabilistic programming languages (PPLs, e.g., Stan, PyMC, Pyro, and Edward) and Bayesian statistical machine learning methods that utilize gradient-information for learning model parameters from data.
A key benefit of AD is that it frees the user of the machine learning methods from providing possibly cumbersome derivatives of the loss function or log posteriors, thereby enabling the training of various and custom machine learning models at scale.
Before explaining further what AD involves, let’s briefly elucidate what is not usually regarded as AD.
Even though AD evaluates derivatives numerically, it is not the same as numerical differentiation via finite difference

Nor is AD meant to be symbolic differentiation where one obtains the exact mathematical expression of the derivative which can lead to an expression swell. That said, some libraries like Tensorflow and Theano/Aesara implement symbolic AD under the hood.
So, what then is normally considered AD?
Simply put, AD is an algorithmic approach to apply the chain rule of differentiation at elementary operation level, storing the values of intermediate steps in memory. One can distinguish two main modes of AD, depending on whether derivatives a computed in a `forward´ or a `backward´ manner when applying the chain rule. These modes are usually called forward-mode AD and reverse-mode AD, respectively.
Both the forward-mode and the reverse-mode rely on the fact that all numerical computations involve compositions of a finite number of elementary operations. These include the arithmetic operations (summation, subtraction, multiplication, and division) and e.g. applying the exponential, logarithm or trigonometric functions. The derivatives of such operations are known. Combining these derivatives via the chain rule then yields the desired total derivative.
Forward-mode automatic differentiation
Forward-mode AD is probably the simpler mode to understand. To be concrete in our description, we consider the evaluation of the derivatives of the two-variable function.
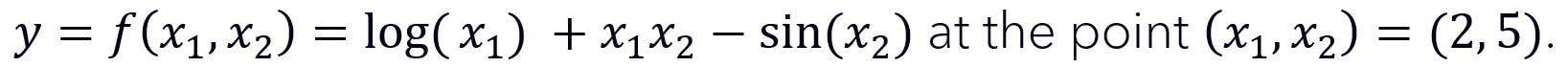
The computation of the value of the function can be illustrated by an evaluation trace (also referred to as a Wengert list) of the elementary operations comprising the function, shown in Figure 1 and the left-hand side of Figure 2.

Which can be computed using the chain rule of differentiation which propagates the derivative trace forward (hence the name of the mode), shown in the right-hand side of Figure 2. Importantly, the derivatives are evaluating during the forward sweep, simultaneously to the variable values.
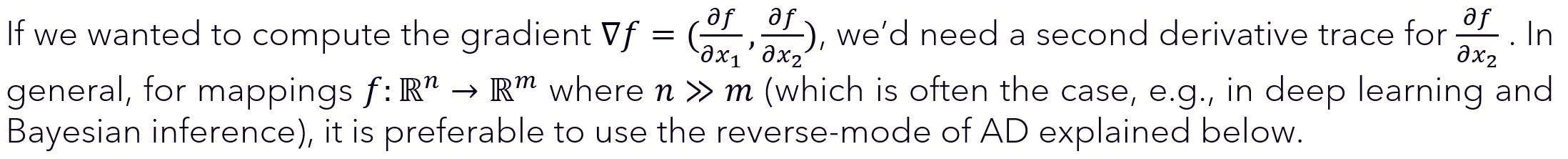
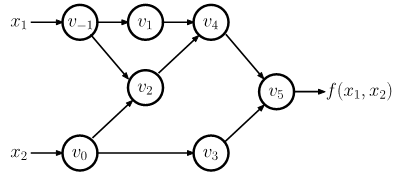
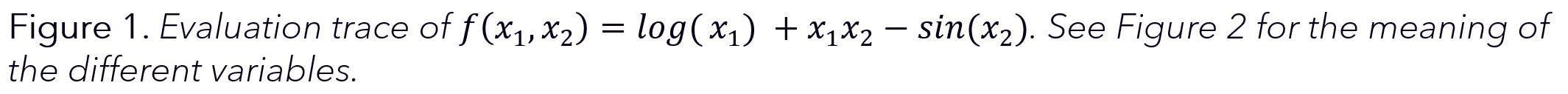
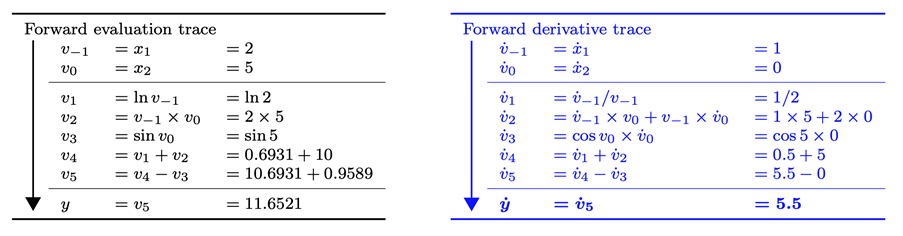
Figure2. Forward-mode AD with evaluation trace of the left and derivative trace on the right. From https://arxiv.org/pdf/1404.7456.pdf
Reverse-mode automatic differentiation
The second main mode of AD seems more complex than the forward mode, but it turns out to be often more useful and efficient in practical settings. In fact, the famous backpropagation algorithm used in training deep neural networks is basically application of reverse-mode AD. In addition, probabilistic programming languages such as Stan and PyMC use the reverse-mode of AD in Bayesian inference.
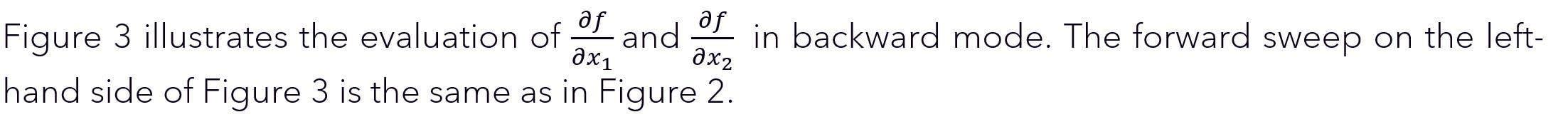
The difference is now that derivatives are not computed during the forward sweep. Instead, derivatives are computed by applying the chain rule in a `backwards´ manner, starting from the final result:


Figure 3. Reverse-mode AD with forward evaluation trace on the left and reverse adjoint (derivative) trace on the right. From https://arxiv.org/pdf/1404.7456.pdf
Automatic differentiation and Bayesian inference
Besides being heavily used in deep learning, automatic differentiation plays a central role in modern Bayesian machine learning techniques such as Hamiltonian Monte Carlo and Automatic Differentiation Variational Inference.
Hamiltonian Monte Carlo (HMC)
Hamiltonian Monte Carlo (HMC) and its No-U-Turn Sampling (NUTS) variant are powerful Markov chain Monte Carlo (MCMC) methods for Bayesian learning for continuous random variables. These methods are implemented, e.g., in the Stan and PyMC probabilistic programming languages.
The sampling in HMC is based on emulating Hamiltonian dynamics in classical mechanics for a fictitious particle with certain position and momentum. Here position represents the random variable of interest (e.g., model parameters, for which we wish to compute posteriors) while momentum is an auxiliary Gaussian random variable to aid the sampling.
Exploration of the state space is done by simulating Hamiltonian dynamics via numerically solving the Hamiltonian equations of motions via leap-frog integration. These Hamiltonian equations of motion require the gradient of the potential energy that plays the role of the negative log posterior. To compute this gradient, probabilistic programming languages employ reverse-mode automatic differentiation.

Since HMC requires the gradient of the log posterior, this also explains why HMC is only applicable for computing posterior distributions of continuous random variables.
While HMC(-NUTS) seems like a complicated way to sample the posterior, it actually turns out to be extremely efficient and fast in practice due to Hamiltonian dynamics being able to avoid random walk behavior displayed by some other MCMC techniques.
Automatic differentiation variational inference (ADVI)
Besides HMC, automatic differentiation can be used in variational inference (VI). The idea of VI is to approximate the complex posterior probability of interest with a simpler one from a family of trial distributions called the variational family.
The unknown parameters of the simpler variational distribution are obtained via maximizing the evidence lower bound (ELBO), which thus turns Bayesian inference into an(stochastic) optimization problem.
Automatic differentiation variational inference (ADVI) is a recent method aiming for automating variational inference at scale by performing much of the technicalities of VI fully under the hood. One of the key techniques in ADVI is applying automatic differentiation to compute the gradient of the ELBO used in the stochastic gradient-ascent optimization.

Libraries for automatic differentiation (and Bayesian inference)
Although many deep learning libraries and probabilistic programming languages take care of gradient computation under the hood, it is sometimes useful to know how to use these libraries for automatic differentiation. If not useful, it’s at least fun and educational.
Reverse-mode AD using the Stan Math Library
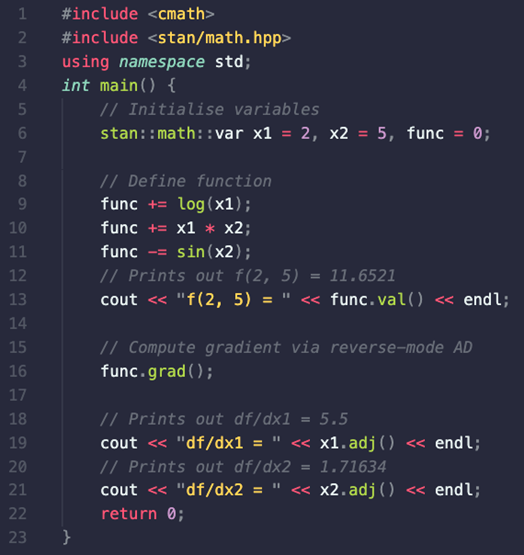
At Sellforte, we use both HMC-NUTS and ADVI as implemented in the probabilistic programming language Stan. Gradient computations for these algorithms are powered by the Stan Math Library which provides an efficient tool to perform reverse-mode AD using C++.
In practice, Stan takes care of computing required derivatives without user intervention. However, it is possible to compute partial derivatives and gradients using the Stan Math Library with just a few lines of C++ code.

Although not necessary from a coding perspective, we define the target function by adding the individual summands one by one for added clarity.
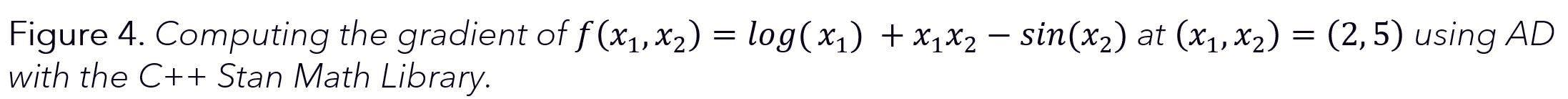
Reverse-mode AD using Aesara
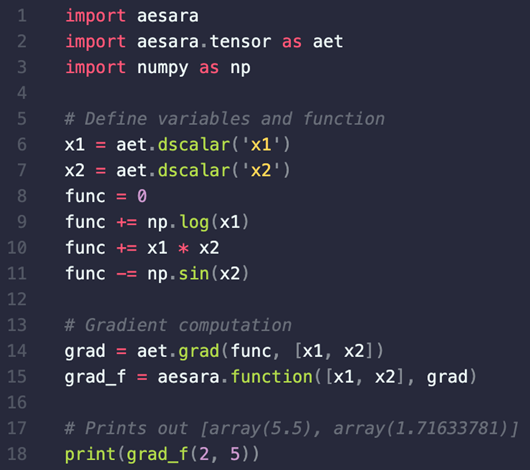
Another popular PPL for Bayesian inference, PyMC, relies on Aesara (a fork of the Theano library) for (symbolic) reverse-mode automatic differentiation. PyMC is a popular alternative to Stan especially for Python users, which is why we give a PyMC-relevant example here.
Like with the Stan Math Library, with Aesara it is also possible to compute the gradient of our example function with just a few lines of code, this time in Python, as shown in Figure 5. For further information on Aesara, we refer to the official documentation.
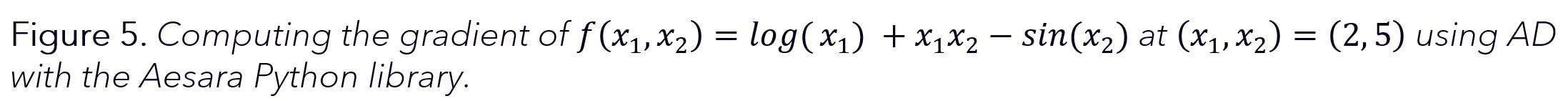
Differentiable programming

-Yann LeCun, via Facebook
Automatic differentiation is a tool that combines different machine learning methods under an umbrella term called differentiable programming.
The concept of differentiable programming has been gaining traction in recent years. Simply put, differentiable programming establishes a framework for various computational approaches, at the core of which lies evaluating gradients of computer programs (representing functions) via AD.
Most notably, deep learning can be seen as a manifestation of this paradigm, as indicated by deep learning pioneer Yann LeCun in 2018. However, gradient-based Bayesian methods such as HMC(-NUTS) and ADVI can also be considered differentiable programming approaches due to the central role of automatic differentiation in them. Differentiable programming thus highlights the similarities between different machine learning methods by bringing gradient-based learning to the forefront.
Final words
In this blog, we gave a brief introduction to automatic differentiation. This technique is prominently used in deep learning and modern Bayesian inference methods as implemented in various PPLs.
Although the used libraries do much of the magic under the hood, it is educational to be aware of the tricks of the trade that make the training of modern machine learning possible at scale.
Automatic differentiation is a huge topic and here we were only able to scratch the surface of the very basics. Nevertheless, knowing the basics of AD is useful in the long and slow journey of learning machine learning and understanding the wider context of new frameworks such as differentiable programming.
Further reading
Atilim Gunes Baydin, Barak A. Pearlmutter. Automatic Differentiation of Algorithms for Machine Learning. arXiv:1404.7456
Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, Jeffrey Mark Siskind. Automatic differentiation in machine learning: a survey. The Journal of Machine Learning Research,18(153):1-43, 2018
Bob Carpenter, Matthew D. Hoffman, Marcus Brubaker, Daniel Lee, Peter Li, Michael Betancourt. The Stan Math Library: Reverse-Mode Automatic Differentiation in C++. arXiv:1509.07164
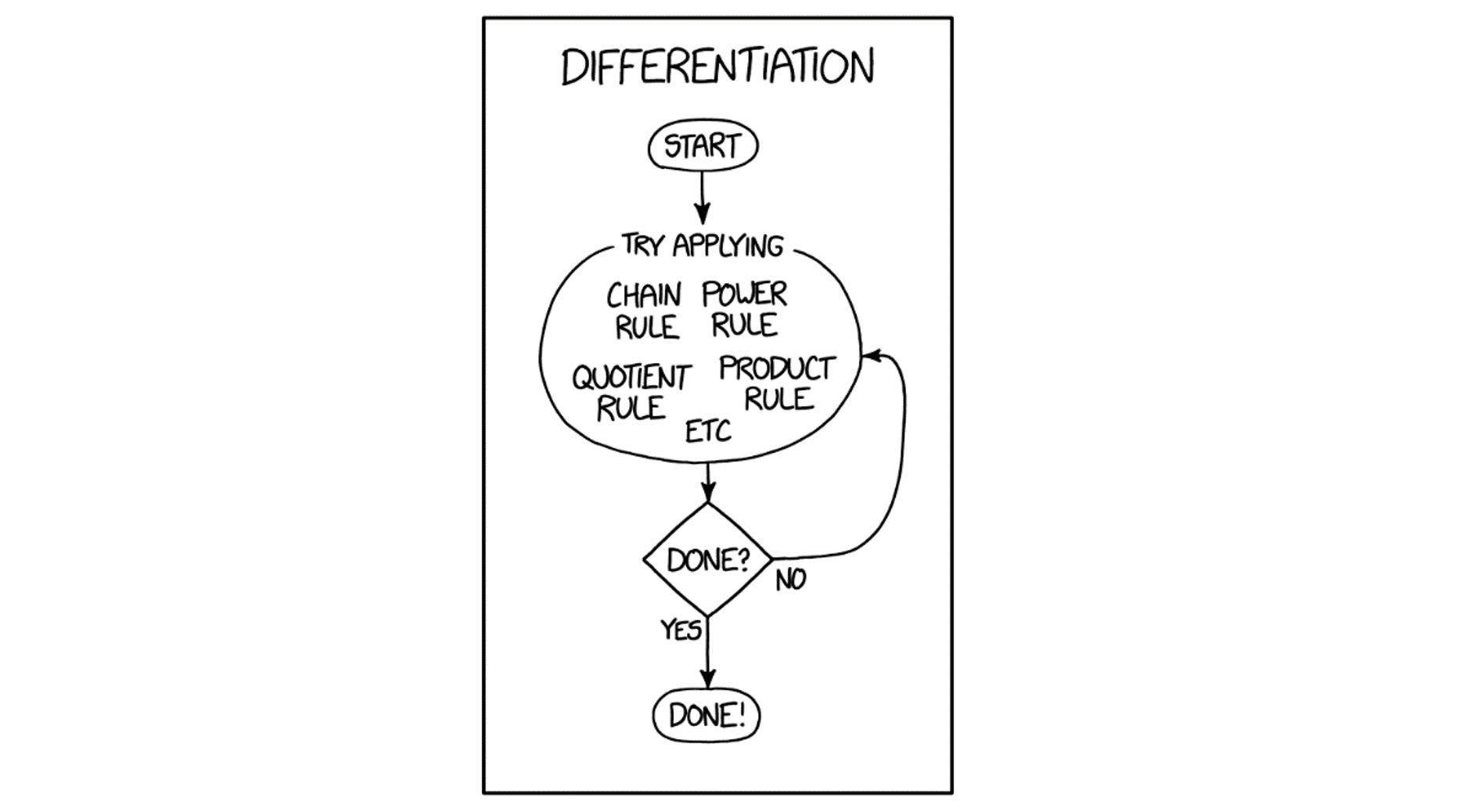
*Main photo adapted from xkcd.
Curious to learn more? Book a demo.
Related articles
Read more postsNo items found!